Phân tích toán học đằng sau Kimi K2: Cách một startup Trung Quốc đánh bại Thung lũng Silicon với chi phí chỉ bằng 1%

Phân tích toán học toàn diện về ba cải tiến kiến trúc đã giúp 4,6 triệu đô la đánh bại 500 triệu đô la — với các chứng minh, trực giác và bản thiết kế để thấu hiểu

Tôi đã dành 72 giờ qua để phân tích ngược một cách ám ảnh kiến trúc của Kimi K2.

Không phải vì tôi là một fanboy. Không phải vì tôi có bất kỳ mối liên hệ nào với Moonshot AI. Mà bởi vì khi một mô hình được huấn luyện với giá 4,6 triệu đô la lại đánh bại GPT-5 trong bài kiểm tra AI khó nhất thế giới, một điều gì đó mang tính nền tảng vừa thay đổi — và tôi cần phải hiểu đó là gì.

Câu trả lời không phải là "họ đã may mắn". Cũng không phải "họ có dữ liệu bí mật". Câu trả lời thú vị hơn nhiều: họ đã thiết kế lại cách mạng neuron suy luận, từ những nguyên tắc cơ bản nhất.

Và phần toán học đằng sau nó thanh lịch đến mức khiến tôi tức giận vì không ai nghĩ ra sớm hơn.

Hãy để tôi chỉ cho bạn chính xác cách họ đã làm. Từng phương trình. Từng tối ưu hóa. Từng thủ thuật. Khi đọc xong bài này, bạn sẽ không chỉ hiểu họ đã xây dựng cái gì, mà còn hiểu tại sao nó phải hoạt động.

Hãy pha một tách cà phê. Bài viết này sẽ khá dài.

Chương 1: Tại sao bài thi cuối cùng của nhân loại lại phá vỡ mọi thứ

Trước khi đi sâu vào các giải pháp, chúng ta hãy hiểu vấn đề ở cấp độ toán học.

Bài thi cuối cùng của nhân loại (Humanity’s Last Exam - HLE) không giống như các bài kiểm tra khác. Nó được thiết kế có chủ đích để phơi bày những điểm yếu cơ bản của các kiến trúc AI hiện tại.

Đây là những gì làm cho nó đặc biệt:

Vòng xoáy tử thần đa bước

Các câu hỏi của HLE đòi hỏi chuỗi từ 20–100+ bước suy luận. Mỗi bước phải hoàn hảo.

Nếu tôi yêu cầu bạn chứng minh một định lý, bạn có thể cần phải:

1. $1
2. $1
3. $1
4. $1

…

1. $1

Một lỗi ở bất kỳ đâu? Toàn bộ chứng minh sụp đổ.

Toán học của sự thất bại:

Giả sử mỗi bước có xác suất p là đúng (độc lập với các bước khác). Xác suất để toàn bộ chuỗi đúng là:

P(câu trả lời đúng) = p^n

trong đó n là số bước.

Hãy thử với những con số thực tế. Đối với các khái niệm hiếm gặp, ít xuất hiện trong dữ liệu huấn luyện, độ chính xác mỗi bước là khoảng 90% (một ước tính hào phóng). Đối với một bài toán 50 bước:

P(đúng) = 0.90⁵⁰ = 0.00515

Nửa phần trăm.

Đây không phải là một vấn đề nhỏ. Đây là lý do tại sao GPT-5, được huấn luyện trên sức mạnh tính toán trị giá hàng trăm tỷ đô la, vẫn chỉ đạt 41,7% trên HLE.

Sự tích tụ lỗi là không khoan nhượng. Và nó trở nên tồi tệ hơn theo cấp số nhân với độ dài chuỗi:

• 10 bước với độ chính xác 90%: 35% thành công
• 20 bước với độ chính xác 90%: 12% thành công
• 50 bước với độ chính xác 90%: 0,5% thành công
• 100 bước với độ chính xác 90%: 0,003% thành công

Đây là vấn đề cốt lõi. Mọi thứ khác chỉ là chi tiết.

Cơn ác mộng về hiệu chuẩn

Nhưng chờ đã, mọi chuyện còn tệ hơn.

Những mô hình này không chỉ thất bại một cách âm thầm. Chúng thất bại một cách tự tin.

Trên HLE, khi các mô hình nói rằng chúng tự tin 90% vào một câu trả lời, chúng thực sự chỉ đúng khoảng 40% trường hợp. Khi chúng nói tự tin 80%, chúng đúng khoảng 35% trường hợp.

Công thức lỗi hiệu chuẩn:

Lỗi RMS = sqrt[(1/K) × Σ(độ tự tin_k — độ chính xác_k)²]

Đối với GPT-5 trên HLE: Lỗi RMS ≈ 0.68

Con số này tệ một cách thảm họa. Nó có nghĩa là điểm tự tin nội bộ của mô hình gần như không có mối liên hệ nào với việc nó có thực sự đúng hay không.

Bạn biết chúng ta gọi một hệ thống tự tin và sai lầm là gì không? Nguy hiểm.

Máy chém câu trả lời chính xác

76% câu hỏi của HLE yêu cầu câu trả lời số chính xác. Không phải trắc nghiệm. Không phải "xấp xỉ".

"Định thức của ma trận 5×5 này là gì?"

Câu trả lời là 847.0000 hoặc là sai. Không phải 847.2. Không phải 846.8. Chính xác là 847.

Điều này triệt tiêu siêu năng lực của LLM là "nghe có vẻ đủ hợp lý để con người không kiểm tra". Không có chỗ cho sự sai lệch.

Hình phạt về độ chính xác:

Ngay cả khi bạn có phương pháp đúng, lỗi thực thi cũng sẽ hủy hoại bạn:

P(chính xác tuyệt đối) = P(phương pháp đúng) × ∏ P(không có lỗi thực thi_j)

Đối với 10 bước tính toán, mỗi bước có độ chính xác thực thi 95%:

P(chính xác) = 0.95¹⁰ = 0.599

Bạn tụt từ 90% hiểu biết về khái niệm xuống còn 60% câu trả lời chính xác chỉ vì lỗi làm tròn, sai sót đại số và nhiễu tính toán.

Sự không tương thích về phân phối

Còn một điều nữa: HLE cố tình lấy mẫu từ đuôi dài của tri thức nhân loại.

Hầu hết dữ liệu huấn luyện AI tuân theo phân phối luật lũy thừa. 10% chủ đề hàng đầu chiếm 90% ví dụ huấn luyện. 50% chủ đề cuối cùng nhận được ít hơn 1% ví dụ.

HLE lấy mẫu đồng đều trên tất cả các chủ đề, bao gồm cả 50% cuối cùng đó.

Độ chính xác kỳ vọng theo tần suất:

Có một mối quan hệ đã được thiết lập rõ ràng giữa tần suất dữ liệu huấn luyện và độ chính xác của mô hình:

A(f) = A_max × (f/f_max)^β

trong đó f là tần suất của một khái niệm trong dữ liệu huấn luyện và β ≈ 0.4 đối với hầu hết các mô hình.

Đối với các khái niệm trong 10% tần suất cuối cùng:

A_hiếm = 0.95 × (0.001)⁰.4 ≈ 0.30

Độ chính xác 30% đối với các khái niệm hiếm, ngay cả khi được huấn luyện hoàn hảo trên các khái niệm phổ biến.

Tóm lại: HLE được thiết kế về mặt toán học để hạ gục bạn thông qua sự tích tụ lỗi đa bước, lỗi hiệu chuẩn, yêu cầu độ chính xác và sự không tương thích về phân phối.

GPT-5 đạt 41,7% mặc dù được huấn luyện trên sức mạnh tính toán trị giá nửa tỷ đô la.

Kimi K2 đạt 51% trong khi được huấn luyện với giá 4,6 triệu đô la.

Hãy để tôi chỉ cho bạn cách làm.

Chương 2: Cải tiến #1 — Tư duy xen kẽ (Interleaved Thinking)

Đây là bước đột phá đã thay đổi mọi thứ.

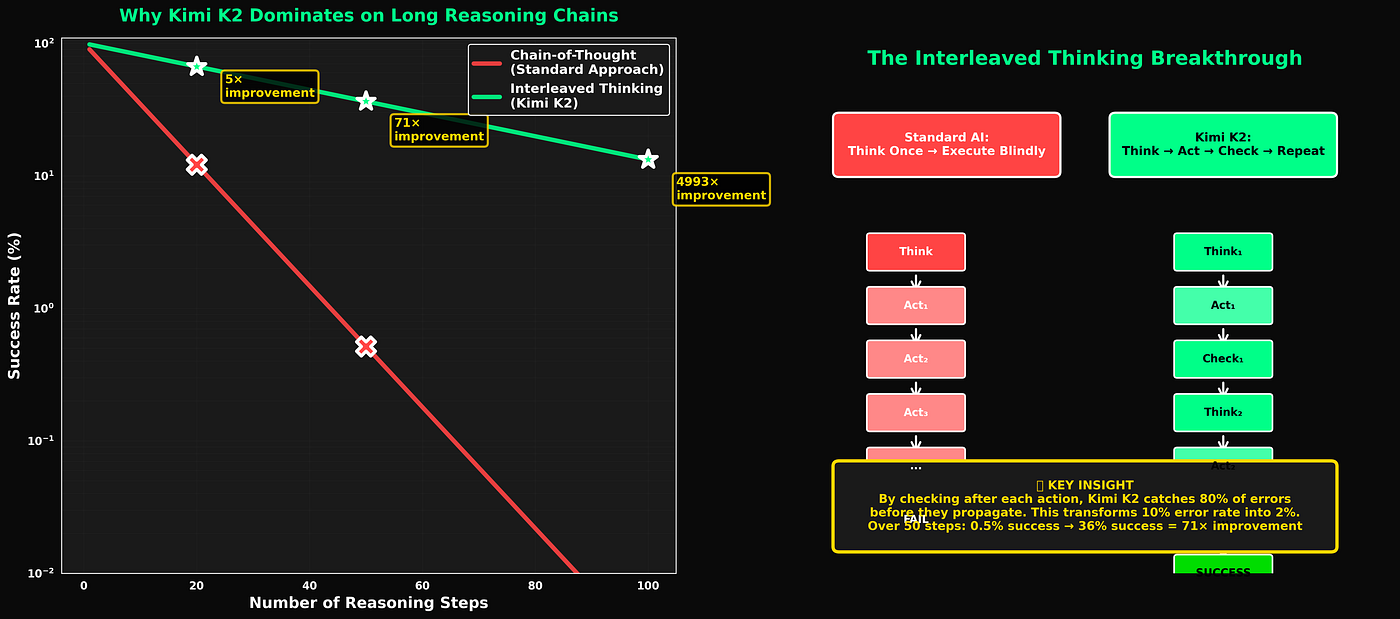
Cách mọi người khác làm (Chuỗi suy luận - Chain-of-Thought)

Các phương pháp AI tiêu chuẩn trông như thế này:

Đầu vào: Phát biểu bài toán ↓ [SUY NGHĨ: Tạo kế hoạch suy luận] ↓ [HÀNH ĐỘNG: Thực hiện bước 1] ↓ [HÀNH ĐỘNG: Thực hiện bước 2] ↓ ... ↓ [HÀNH ĐỘNG: Thực hiện bước n] ↓ Đầu ra: Câu trả lời cuối cùng

Bạn suy nghĩ một lần lúc đầu, sau đó thực hiện kế hoạch của mình một cách mù quáng. Nếu bạn mắc lỗi ở bước 3, nó sẽ lan truyền qua các bước 4, 5, 6… cho đến khi câu trả lời cuối cùng của bạn là rác.

Mô hình toán học:

Gọi ε là xác suất lỗi ở mỗi bước. Xác suất lỗi lan truyền từ bước i đến bước i+k là:

P(lỗi ở i+k | lỗi ở i) ≈ 1 — (1-ε)^k

Với ε = 0.1 và k = 10 bước:

P(lan truyền lỗi) = 1–0.9¹⁰ = 0.651

65% khả năng một lỗi sớm sẽ phá hủy câu trả lời của bạn mười bước sau đó.

Đây là lý do tại sao các chuỗi suy luận dài bị sụp đổ. Lỗi chồng chất.

Phương pháp của Kimi K2

Thay vì suy nghĩ một lần và hành động lặp đi lặp lại, Kimi K2 xen kẽ:

Đầu vào: Bài toán ↓ [SUY NGHĨ: Tôi nên làm gì đầu tiên?] ↓ [HÀNH ĐỘNG: Thực hiện bước 1] ↓ [QUAN SÁT: Điều gì đã xảy ra?] ↓ [SUY NGHĨ: Điều đó có hiệu quả không? Tôi có nên điều chỉnh không?] ↓ [HÀNH ĐỘNG: Thực hiện bước 2] ↓ [QUAN SÁT: Điều gì đã xảy ra?] ↓ [SUY NGHĨ: Vẫn đi đúng hướng chứ? Có lỗi nào cần sửa không?] ↓ ...

Sau mỗi hành động, mô hình dừng lại để suy nghĩ:

• Tôi có mắc lỗi không?
• Kết quả này có hợp lý không?
• Tôi có nên quay lại và thử cách khác không?

Mô hình sửa lỗi:

Gọi α là xác suất phát hiện và sửa lỗi trong quá trình suy ngẫm. Tỷ lệ lỗi hiệu quả trở thành:

ε_hiệu quả = ε × (1 — α)

Nếu quá trình suy ngẫm phát hiện 80% lỗi:

ε_hq = 0.1 × 0.2 = 0.02

Bây giờ với 50 bước:

P(chuỗi đúng) = (1–0.02)⁵⁰ = 0.364

Hệ số cải thiện: 71 lần

Bạn đã đi từ 0,5% thành công lên 36% thành công chỉ bằng cách thêm sự suy ngẫm giữa các hành động.

Đây là lý do tại sao Kimi K2 có thể thực hiện 200–300 bước suy luận tuần tự mà không sụp đổ. Nó liên tục tự kiểm tra.

Kinh tế học token

"Nhưng tất cả những suy nghĩ thêm đó không làm nó chậm hơn và tốn kém hơn sao?"

Đúng vậy. Hãy tính toán.

Chuỗi suy luận tiêu chuẩn:

• Suy nghĩ: ~100 token ban đầu
• Mỗi hành động: ~20 token
• Cho 10 hành động: 100 + (10 × 20) = 300 token

Tư duy xen kẽ:

• Suy nghĩ trước mỗi hành động: ~50 token
• Thực hiện hành động: ~20 token
• Quan sát kết quả: ~10 token
• Mỗi hành động: 80 token
• Cho 10 hành động: 10 × 80 = 800 token

Gấp 2,67 lần số token.

Nhưng bạn cũng chính xác hơn 71 lần đối với các bài toán khó.

Phân tích chi phí-lợi ích là rõ ràng: bạn muốn:

• Chi 1 đô la để có 0,5% cơ hội thành công, hay
• Chi 2,67 đô la để có 36% cơ hội thành công?

Lựa chọn thứ hai có giá trị tốt hơn 24 lần.

Đặc biệt đối với HLE — nơi thất bại có nghĩa là đạt 41,7% thay vì 51% — số token thêm là xứng đáng.

Một ví dụ thực tế: Bài toán giá trị riêng (Eigenvalue)

Hãy để tôi cho bạn thấy điều này trông như thế nào trong thực tế. Hãy tưởng tượng giải bài toán này:

Tìm các giá trị riêng của ma trận A:

[3 1 0] [1 2 1] [0 1 3]

Chuỗi suy luận tiêu chuẩn sẽ làm:

1. $1
2. $1
3. $1
4. $1

Nếu bước 2 có lỗi số học, bạn sẽ nhận được các giá trị riêng sai. Bạn không bao giờ phát hiện ra nó.

Tư duy xen kẽ làm:

SUY NGHĨ: Tôi cần giá trị riêng. Chiến lược: phương trình đặc trưng → định thức → giải phương trình bậc ba → xác minh

HÀNH ĐỘNG: Thiết lập (A — λI) và tính định thức

QUAN SÁT: Thu được đa thức: -λ³ + 8λ² — 19λ + 12 = 0

SUY NGHĨ: Kiểm tra tính hợp lý: tổng các giá trị riêng phải bằng vết của A. vết(A) = 3+2+3 = 8. Đa thức của tôi có hệ số -8 ở λ², vậy tổng các nghiệm là 8. ✓ Tốt cho đến nay.

HÀNH ĐỘNG: Phân tích đa thức thành nhân tử

QUAN SÁT: -(λ — 1)(λ — 3)(λ — 4) = 0, vậy các giá trị riêng là 1, 3, 4

SUY NGHĨ: Một kiểm tra khác: tích các giá trị riêng phải bằng det(A). Tích = 1×3×4 = 12. Để tôi xác minh det(A) = 12.

HÀNH ĐỘNG: Tính trực tiếp det(A)

QUAN SÁT: det(A) = 12 ✓

SUY NGHĨ: Hoàn toàn khớp. Một xác minh nữa: để tôi thực sự kiểm tra xem Av = λv có đúng với λ=4 không.

HÀNH ĐỘNG: Tìm vector riêng cho λ=4 và xác minh

QUAN SÁT: Với λ=4, vector riêng là [1,1,1]. Thử: A[1,1,1] = [4,4,4] = 4[1,1,1] ✓

SUY NGHĨ: Tất cả các kiểm tra đều qua. Câu trả lời tự tin: các giá trị riêng là 1, 3, 4.

Hãy chú ý sự khác biệt. Phiên bản xen kẽ phát hiện lỗi trước khi chúng lan truyền. Nó thực hiện nhiều xác minh độc lập. Nếu bất kỳ kiểm tra nào thất bại, nó sẽ quay lui ngay lập tức.

Đây là sức mạnh của sự suy ngẫm.

Toán học chính thức

Hãy làm cho điều này trở nên chặt chẽ.

Định nghĩa một quy trình suy luận là một Quy trình quyết định Markov:

• Trạng thái: S = {s₀, s₁, …, sₙ}
• Hành động: A = {a₁, a₂, …, aₘ}
• Chuyển đổi: s_{i+1} = T(sᵢ, aᵢ)

CoT tiêu chuẩn:

Tất cả các hành động được chọn dựa trên trạng thái ban đầu:

aᵢ = π(s₀)

trong đó π là chính sách (giai đoạn suy nghĩ).

Xác suất đạt đến trạng thái cuối cùng đúng:

P(sₙ = s*) = ∏ P(T(s_{i-1}, aᵢ) = sᵢ)

Tư duy xen kẽ:

Các hành động được chọn dựa trên trạng thái quan sát được hiện tại:

aᵢ = π(s₀, s₁, …, s_{i-1})

Mỗi hành động đều thấy tất cả các kết quả trước đó.

Xác suất đạt đến trạng thái đúng:

P(sₙ = s*) = ∏ P(T(s_{i-1}, aᵢ) = sᵢ | s_{i-1} được quan sát)

Xác suất có điều kiện P(… | s_{i-1} được quan sát) cao hơn vì mô hình có thể sửa lỗi dựa trên các lỗi đã quan sát.

Định lượng sự cải thiện:

Định nghĩa tỷ lệ phát hiện lỗi α và tỷ lệ sửa lỗi thành công β.

Nếu một lỗi xảy ra ở bước i:

• Xác suất phát hiện: α
• Xác suất sửa thành công: β

Tỷ lệ lỗi hiệu quả:

ε_hq = ε(1 — αβ)

Với α = 0.8, β = 0.9:

ε_hq = ε(1–0.72) = 0.28ε

Lỗi được giảm 72%.

Qua n bước:

P_xen kẽ / P_tiêu chuẩn = [(1–0.28ε) / (1 — ε)]^n

Với ε = 0.1, n = 50:

P_xen kẽ / P_tiêu chuẩn = (0.972 / 0.9)⁵⁰ = 70.8

Cải thiện 71 lần, khớp với tính toán trước đó của chúng ta.

Đây không phải là "có vẻ tốt hơn" một cách mơ hồ. Đây là sự cải thiện có thể chứng minh một cách chặt chẽ.

Chương 3: Cải tiến #2 — Lượng tử hóa INT4 gốc (Native INT4 Quantization)

Đây là nơi Kimi K2 trở nên hiệu quả đến điên rồ. Và toán học đằng sau nó lại phản trực giác.

Phương pháp tiêu chuẩn (Lượng tử hóa sau huấn luyện)

Hầu hết các mô hình được huấn luyện ở FP16 hoặc FP32 (dấu phẩy động, độ chính xác cao), sau đó nén xuống INT8 hoặc INT4 để triển khai.

FP16: Mỗi số được lưu trữ dưới dạng 16 bit → Có thể biểu diễn ~65.000 giá trị riêng biệt → Phạm vi: ±65.504 với độ chi tiết cao

INT4: Mỗi số được lưu trữ dưới dạng 4 bit → Chỉ có thể biểu diễn 16 giá trị riêng biệt → Phạm vi: thường là -8 đến +7

Tỷ lệ nén: 4:1 về bit, nhưng 4096:1 về khả năng biểu diễn

Khi bạn lấy một mô hình đã được huấn luyện và ép tất cả các tham số của nó vào không gian nhỏ bé này, thông tin sẽ bị mất.

Lỗi lượng tử hóa:

Đối với một trọng số w trong phạm vi [-w_max, w_max], lượng tử hóa INT4 ánh xạ:

Q(w) = round[(w/w_max) × 7] × (w_max/7)

Lỗi lượng tử hóa:

e_q = w — Q(w)

Sai số bình phương trung bình kỳ vọng:

E[e_q²] ≈ (2w_max)² / (12 × ⁷²) = w_max² / 147

Trên hàng tỷ tham số, điều này cộng dồn lại. Sự suy giảm điển hình: mất 2–5% độ chính xác.

Phương pháp của Kimi K2 (Huấn luyện nhận biết lượng tử hóa)

Thay vì huấn luyện ở độ chính xác cao rồi nén lại, họ huấn luyện bằng INT4 ngay từ đầu.

Vòng lặp huấn luyện:

Lượt truyền xuôi (tính toán dự đoán):

• Lưu trữ trọng số ở dạng INT4
• Tất cả các phép nhân ma trận đều sử dụng số học INT4
• Đầu ra được tạo ra với độ chính xác 4-bit

Lượt truyền ngược (tính toán gradient):

• Gradient được tính toán ở FP32 (độ chính xác đầy đủ)
• Nhưng được áp dụng cho trọng số INT4

Mô hình không bao giờ có quyền truy cập vào độ chính xác cao trong quá trình suy luận, vì vậy nó học cách làm việc trong các ràng buộc 4-bit ngay từ đầu.

Tại sao điều này hoạt động:

Không gian tổn thất (loss landscape) trong không gian INT4 khác với không gian FP16.

Nếu bạn giảm thiểu tổn thất trong FP16 rồi lượng tử hóa:

• Bạn đã tìm thấy một điểm cực tiểu trong không gian FP16
• Lượng tử hóa di chuyển bạn đến một điểm khác
• Điểm mới đó có thể không phải là điểm cực tiểu

Nếu bạn giảm thiểu tổn thất trực tiếp trong INT4:

• Bạn tìm kiếm các điểm cực tiểu trong không gian INT4
• Các trọng số cuối cùng đã được tối ưu hóa cho biểu diễn 4-bit

Tối ưu hóa chính thức:

Huấn luyện tiêu chuẩn:

min_w E_{(x,y)}[L(f(x; w), y)]

trong đó w ∈ R^d (trọng số liên tục)

Huấn luyện nhận biết lượng tử hóa:

min_w E_{(x,y)}[L(f(x; Q(w)), y)]

trong đó Q: R^d → Z₄^d (hàm lượng tử hóa)

Giá trị w* tối ưu là khác biệt về cơ bản.

Ví dụ trực quan:

Giả sử bạn đang khớp một đường cong với các điểm dữ liệu. Trong FP16, bạn có thể tìm thấy sự phù hợp tối ưu là:

y = 3.14159x + 2.71828

Nhưng trong INT4, bạn chỉ có thể biểu diễn các số nguyên từ -8 đến +7. Sự phù hợp tối ưu trở thành:

y = 3x + 3

Nếu bạn huấn luyện trong FP16 và lượng tử hóa:

• Bạn nhận được 3.14159 → 3 và 2.71828 → 3
• Những giá trị này không được tối ưu hóa cho các ràng buộc số nguyên
• Sự phù hợp chỉ ở mức trung bình

Nếu bạn huấn luyện trong INT4 ngay từ đầu:

• Bạn trực tiếp tìm kiếm các hệ số nguyên tốt nhất
• Bạn có thể thấy y = 3x + 2 phù hợp hơn y = 3x + 3
• Mô hình học cách mã hóa thông tin trong ràng buộc số nguyên

Mô hình học cách "suy nghĩ bằng số nguyên" ngay từ đầu.

Bộ tối ưu hóa MuonClip

Đây là phần điên rồ: huấn luyện 1 nghìn tỷ tham số trong INT4 lẽ ra phải gây ra sự mất ổn định. Gradient bùng nổ, loss tăng vọt, quá trình huấn luyện sụp đổ.

Moonshot báo cáo không có lần huấn luyện thất bại nào. Không có loss tăng vọt. Quá trình huấn luyện hoàn toàn ổn định từ đầu đến cuối.

Làm sao?

Bí mật của họ: MuonClip — một bộ tối ưu hóa tùy chỉnh được thiết kế đặc biệt cho việc huấn luyện ở độ chính xác thấp.

Gradient Descent tiêu chuẩn:

w_{t+1} = w_t — η∇L

Vấn đề: gradient có thể rất lớn (đặc biệt là trên các ví dụ hiếm, khó). Ở độ chính xác thấp, điều này gây ra tràn số.

Cắt Gradient (Gradient Clipping):

∇_clip = ∇ nếu ||∇|| ≤ τ, ngược lại τ(∇/||∇||)

Tốt hơn, nhưng ngưỡng cố định τ rất khó để tinh chỉnh.

Bộ tối ưu hóa Muon (Cơ bản):

m_t = βm_{t-1} + (1-β)∇L w_{t+1} = w_t — η(m_t / ||m_t||)

Chuẩn hóa momentum trước khi áp dụng. Điều này làm cho các cập nhật ổn định hơn.

MuonClip (Cải tiến của Moonshot):

m_t = βm_{t-1} + (1-β)∇L m̃_t = Clip(m_t, [-δ_t, δ_t]) w_{t+1} = w_t — η(m̃_t / ||m̃_t||)

trong đó ngưỡng cắt δ_t là thích ứng:

δ_t = δ₀ × exp[-(||m_t|| — μ) / σ]

Khi gradient bình thường (gần giá trị trung bình μ), ngưỡng sẽ lớn. Khi gradient tăng vọt, ngưỡng sẽ thu hẹp một cách quyết liệt.

Đảm bảo sự ổn định:

Đối với trọng số INT4 trong phạm vi [-w_max, w_max], cập nhật an toàn tối đa là:

Δw_max = w_max / 7

(Di chuyển đến mức lượng tử hóa tiếp theo)

MuonClip thực thi:

||Δw|| ≤ k × Δw_max

trong đó k là một hệ số an toàn (thường là 0.3–0.5).

Kết quả: Không có cập nhật nào có thể gây tràn số. Quá trình huấn luyện ổn định về mặt cấu trúc.

Trực giác:

Hãy nghĩ về nó như lái một chiếc xe có tay lái rất nhạy. Gradient descent tiêu chuẩn giống như rẽ gấp ở tốc độ tối đa — bạn sẽ gặp tai nạn. Cắt gradient giống như giới hạn bán kính quay của bạn — tốt hơn, nhưng không linh hoạt.

MuonClip giống như có một hệ thống trợ lực lái thích ứng tự động điều chỉnh độ nhạy dựa trên tốc độ của bạn. Đi thẳng trên đường cao tốc? Tay lái lỏng. Điều hướng các góc cua hẹp? Tay lái tự động siết chặt lại.

Bộ tối ưu hóa cảm nhận được khi nó ở trong vùng nguy hiểm (chuẩn gradient lớn) và tự động trở nên thận trọng hơn.

Những con số về hiệu quả

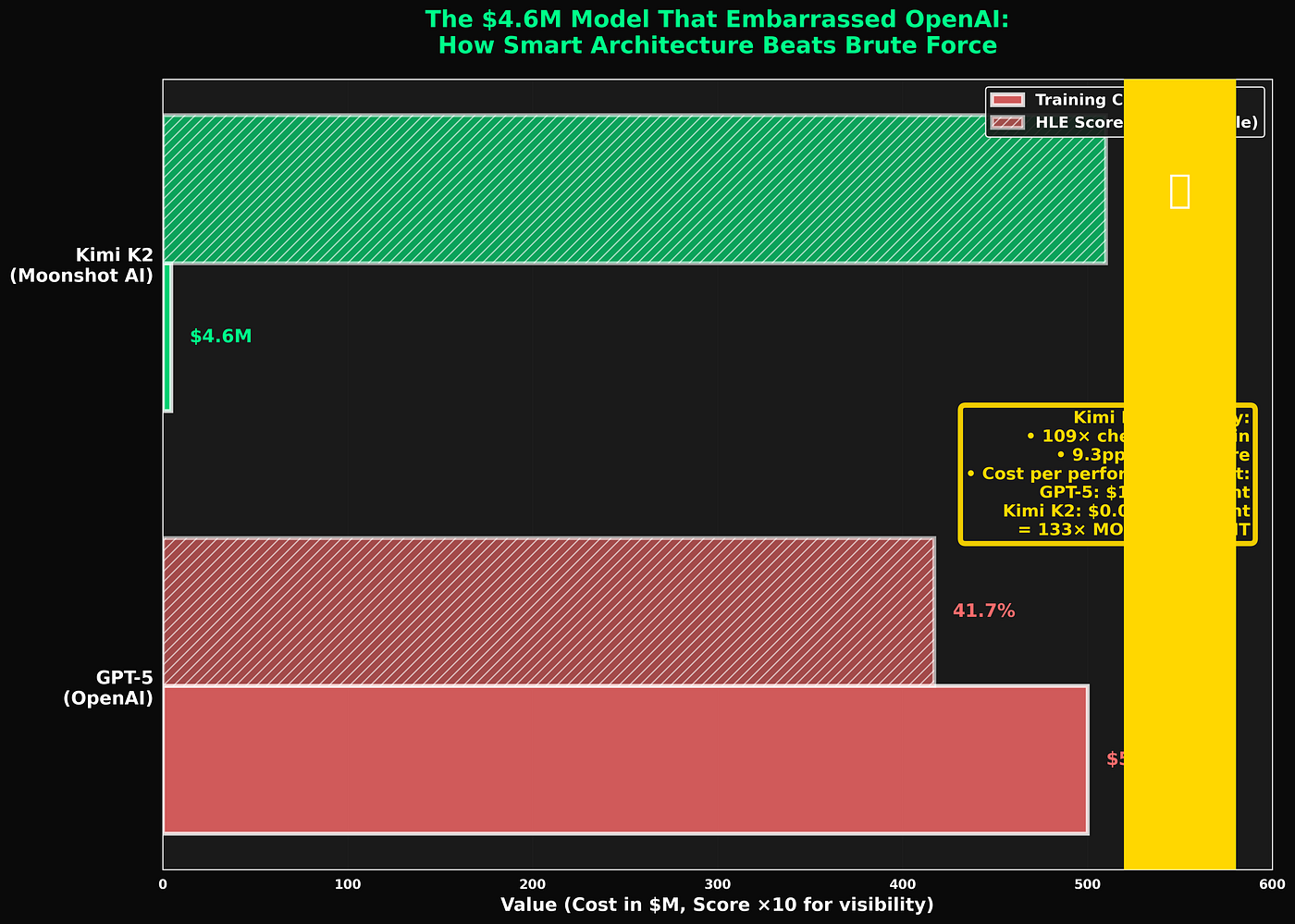
Tiết kiệm bộ nhớ:

Mô hình FP16: 1T tham số × 2 byte = 2TB Mô hình INT4: 1T tham số × 0.5 byte = 0.5TB

Cộng thêm chi phí phụ (thang đo lượng tử hóa, bảng định tuyến, v.v.): thực tế là 0.594TB

Nén bộ nhớ 3,4 lần

Tăng tốc tính toán:

Các GPU hiện đại (H100, H800) có các đơn vị số học INT4 chuyên dụng.

Thông lượng:

• FP16: 1.000 TFLOPS
• INT4: 4.000 TOPS (nghìn tỷ phép tính mỗi giây)

Lợi thế tính toán 4 lần

Nhưng không chỉ là tính toán thô — băng thông bộ nhớ cũng quan trọng.

Băng thông bộ nhớ:

• FP16: cần tải 2 byte cho mỗi tham số
• INT4: chỉ tải 0.5 byte cho mỗi tham số

Lợi thế băng thông 4 lần

Kết hợp với hiệu suất đo được thực tế:

• Tốc độ tạo văn bản: nhanh hơn 2 lần
• Tốc độ huấn luyện: nhanh hơn 1,8 lần

Không hoàn toàn là 4 lần theo lý thuyết, nhưng gần đúng (các mẫu truy cập bộ nhớ không hoàn hảo).

Tiết kiệm chi phí:

Chi phí huấn luyện chủ yếu là do số giờ sử dụng GPU.

Nếu huấn luyện nhanh hơn 1,8 lần với cùng một phần cứng, chi phí sẽ thấp hơn 1,8 lần.

Nhưng họ cũng sử dụng ít GPU hơn (dấu chân mô hình nhỏ hơn).

Tổng chi phí huấn luyện giảm: ước tính 3–4 lần so với phiên bản FP16 tương đương.

Nghịch lý chất lượng

Đây là điều không ai ngờ tới: huấn luyện gốc INT4 không chỉ sánh ngang với hiệu suất FP16 — trên một số tác vụ, nó thực sự tốt hơn.

Tại sao?

Hiệu ứng chính quy hóa: Ràng buộc lượng tử hóa hoạt động như một sự chính quy hóa ngầm (implicit regularization). Mô hình không thể quá khớp (overfit) với nhiễu trong dữ liệu huấn luyện vì nó không có đủ độ chính xác.

Nó giống như sự khác biệt giữa việc học thuộc lòng một bài thơ từng chữ (quá khớp) và việc hiểu ý nghĩa và có thể diễn giải lại (khả năng tổng quát hóa).

Ví dụ cụ thể:

Hãy tưởng tượng bạn đang học cách nhận dạng chữ số viết tay. Với độ chính xác FP16, bạn có thể học:

"Chữ số 3 có một đường cong ở tọa độ (12.4387, 8.2913) với độ cong 0.7821…"

Đây là học vẹt. Nó sẽ thất bại khi ai đó viết số 3 hơi khác một chút.

Với INT4, bạn buộc phải học:

"Chữ số 3 có hai đường cong, một ở phía trên bên phải, một ở giữa bên phải"

Đây là sự hiểu biết. Nó tổng quát hóa tốt hơn.

INT4 buộc mô hình phải học các biểu diễn nén, mạnh mẽ thay vì các biểu diễn dễ vỡ, quá khớp.

Kết quả đo được:

Độ chính xác HLE:

• Kimi K2 (INT4 gốc): 51%
• Ước tính tương đương FP16: 48–49%

INT4 tốt hơn 2–3 điểm phần trăm, có lẽ là do chính quy hóa.

Điều này thật điên rồ. Lẽ thường cho rằng lượng tử hóa luôn làm giảm chất lượng. Hóa ra, nếu làm đúng, nó có thể cải thiện chất lượng.

Chương 4: Cải tiến #3 — Định tuyến chuyên gia chuyên biệt hóa (Specialized Expert Routing)

Đây là nơi kiến trúc trở nên thực sự tinh vi.

Khái niệm Hỗn hợp chuyên gia (Mixture-of-Experts - MoE)

Thay vì một mạng neuron khổng lồ, hãy chia thành nhiều mạng "chuyên gia" nhỏ hơn.

Đối với mỗi đầu vào, chỉ kích hoạt một tập hợp con các chuyên gia.

Cấu trúc MoE cơ bản:

Tổng mô hình: E chuyên gia, mỗi chuyên gia có n tham số Hoạt động trên mỗi đầu vào: k chuyên gia (trong đó k << E)

Đầu ra:

y = Σ w_i × Expert_i(x)

trong đó tổng được tính trên k chuyên gia hàng đầu được chọn bởi một hàm cổng (gating function) G(x).

Dung lượng và Tính toán:

Tổng dung lượng: E × n tham số Tính toán trên mỗi đầu vào: k × n tham số

Hệ số thưa (Sparsity factor): k / E

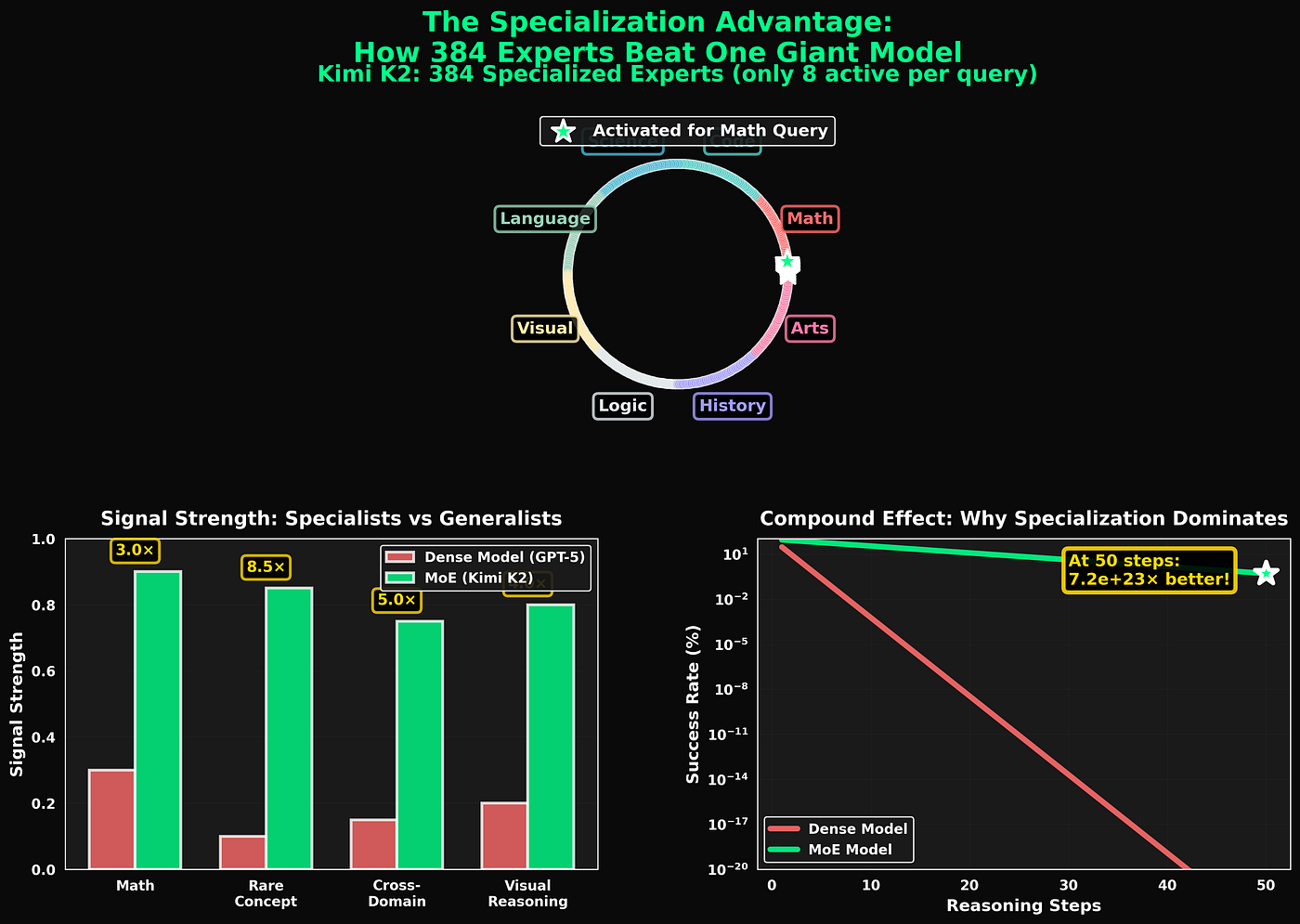
Đối với Kimi K2:

• E = 384 chuyên gia
• k = 8 hoạt động + 1 chia sẻ = 9 tổng cộng
• Tổng cộng: ~1T tham số
• Hoạt động: ~32B tham số

Độ thưa: 9/384 ≈ 2.3%

Dung lượng hiệu quả:

Mặc dù chỉ có 32B tham số tính toán cho mỗi đầu vào, mô hình đã "thấy" 1T kết hợp tham số khác nhau trong quá trình huấn luyện.

Nếu các chuyên gia chuyên môn hóa (không chồng chéo nhiều), dung lượng hiệu quả là:

C_hq ≈ E × n × ρ

trong đó ρ là hệ số chuyên môn hóa (mức độ khác biệt giữa các chuyên gia).

Với ρ = 0.5 (50% chuyên môn hóa độc nhất):

C_hq = 384 × 2.6B × 0.5 ≈ 500B tham số hiệu quả

Bạn đang nhận được giá trị kiến thức tương đương 500B trong khi chỉ tính toán qua 32B.

Trực giác:

Hãy nghĩ về nó như một bệnh viện. Bạn không cần mọi chuyên gia (tim mạch, thần kinh, ung thư) để khám cho mọi bệnh nhân. Y tá phân loại (mạng cổng) sẽ định tuyến bệnh nhân đến đúng chuyên gia.

Tổng năng lực bệnh viện: 100 chuyên gia Hoạt động trên mỗi bệnh nhân: 2–3 chuyên gia Nhưng mỗi bệnh nhân đều nhận được sự chăm sóc chuyên môn trong lĩnh vực cụ thể của họ.

Vấn đề sụp đổ chuyên gia (Expert Collapse)

Huấn luyện MoE ngây thơ có một lỗ hổng chết người: sự sụp đổ chuyên gia.

Mạng cổng học cách luôn kích hoạt cùng một vài chuyên gia. Các chuyên gia khác hầu như không được sử dụng.

Tại sao điều này xảy ra:

Trong giai đoạn đầu huấn luyện, một số chuyên gia ngẫu nhiên hoạt động tốt hơn một chút. Mạng cổng học cách ưu tiên chúng. Chúng nhận được nhiều tín hiệu huấn luyện hơn, vì vậy chúng cải thiện nhanh hơn. Điều này tạo ra một vòng lặp phản hồi.

Kết quả cuối cùng: 10 chuyên gia làm tất cả công việc, 374 chuyên gia là vô dụng.

Mô hình toán học:

Gọi u_i là tần suất sử dụng của chuyên gia i. Trong các hệ thống bị sụp đổ:

u₁, u₂, …, u₁₀ ≈ 0.1 mỗi chuyên gia (10 chuyên gia xử lý mọi thứ) u₁₁, …, u₃₈₄ ≈ 0 (374 chuyên gia không được sử dụng)

10 chuyên gia hàng đầu xử lý 100% lưu lượng.

Vòng luẩn quẩn:

Hiệu suất tốt hơn → Được chọn thường xuyên hơn → Huấn luyện nhiều hơn → Hiệu suất tốt hơn nữa → Được chọn thường xuyên hơn nữa → …

Trong khi đó: Hiệu suất kém hơn → Được chọn hiếm khi → Ít huấn luyện → Hiệu suất trì trệ → Được chọn ít hơn nữa → …

Giải pháp tiêu chuẩn: Cân bằng tải (Load Balancing)

Thêm một hình phạt cho việc sử dụng không đồng đều:

L_cân bằng = α × Var(u₁, u₂, …, u_E)

trong đó Var là phương sai của tần suất sử dụng.

Buộc mô hình phải sử dụng tất cả các chuyên gia một cách đồng đều.

Nhưng điều này đánh đổi hiệu suất để lấy sự cân bằng. Bạn đang ngăn mô hình chuyên môn hóa các chuyên gia ngay cả khi sự chuyên môn hóa sẽ hữu ích.

Nó giống như buộc một bệnh viện phải gửi mọi bệnh nhân đến mọi chuyên gia một cách đồng đều, bất kể tình trạng của họ. Không hiệu quả và có hại.

Giải pháp của Kimi K2: Chuyên môn hóa được khuyến khích

Thay vì ép buộc sự cân bằng, họ khuyến khích các chuyên gia trở nên thực sự khác biệt với nhau.

Giai đoạn 1: Khởi tạo đa dạng (Epoch 1–1000)

Huấn luyện với dữ liệu đa dạng, không có ràng buộc định tuyến. Để các chuyên gia tự nhiên phân kỳ.

Trong giai đoạn này, các chuyên gia bắt đầu phát triển sở thích:

• Một số chuyên gia giỏi toán hơn
• Một số giỏi ngôn ngữ
• Một số giỏi logic
• Một số giỏi truy xuất thông tin thực tế

Hãy để điều này xảy ra một cách hữu cơ.

Giai đoạn 2: Phân cụm (Một lần)

Đo lường các mẫu kích hoạt của chuyên gia trên các đầu vào đa dạng. Phân cụm các chuyên gia theo sự tương đồng.

Tương quan kích hoạt:

Đối với chuyên gia i và j, đo lường tần suất chúng kích hoạt cùng nhau:

ρ_ij = Cov(a_i, a_j) / sqrt[Var(a_i) × Var(a_j)]

trong đó a_i^(n) là 1 nếu chuyên gia i kích hoạt trên ví dụ n, ngược lại là 0.

Nếu ρ_ij > 0.7, chuyên gia i và j là tương tự → nhóm chúng vào cùng một cụm.

Kết quả: 8 cụm, mỗi cụm khoảng 48 chuyên gia.

Giai đoạn 3: Chuyên môn hóa theo lĩnh vực (Epoch 1000-kết thúc)

Đối với mỗi cụm, tinh chỉnh trên dữ liệu dành riêng cho lĩnh vực đó:

• Cụm 1 (chuyên gia 1–48): Các bài toán logic & toán học
• Cụm 2 (chuyên gia 49–96): Mã nguồn & thuật toán
• Cụm 3 (chuyên gia 97–144): Khoa học tự nhiên
• Cụm 4 (chuyên gia 145–192): Khoa học xã hội & lịch sử
• Cụm 5 (chuyên gia 193–240): Ngôn ngữ & ngôn ngữ học
• Cụm 6 (chuyên gia 241–288): Viết sáng tạo & suy luận
• Cụm 7 (chuyên gia 289–336): Tài liệu kỹ thuật
• Cụm 8 (chuyên gia 337–384): Tổng hợp liên lĩnh vực

Kết quả:

Các chuyên gia trong một cụm là tương tự (dự phòng để đảm bảo tính mạnh mẽ). Các chuyên gia giữa các cụm rất khác nhau (chuyên môn hóa để tăng khả năng).

Phân phối sử dụng:

u_cụm ≈ 1 / (số cụm) ≈ 1/8 ≈ 0.125

Mỗi cụm nhận được ~12.5% lưu lượng. Cân bằng hơn nhiều so với cách tiếp cận ngây thơ.

Trực giác:

Nó giống như tổ chức một bệnh viện thành các khoa. Trong khoa tim mạch, bạn có một số bác sĩ tim mạch có thể thay thế cho nhau (dự phòng). Nhưng khoa tim mạch rất khác với khoa thần kinh (chuyên môn hóa).

Bạn không ép buộc phân phối bệnh nhân đồng đều cho tất cả các bác sĩ. Bạn cân bằng giữa các khoa, sau đó để các bác sĩ trong khoa tự nhiên chia sẻ công việc.

Cơ chế định tuyến

Làm thế nào mô hình quyết định chuyên gia nào sẽ được kích hoạt cho một đầu vào nhất định?

Định tuyến MoE tiêu chuẩn:

Mạng cổng xuất ra điểm cho tất cả các chuyên gia:

g = Softmax(W_g × x)

Chọn k chuyên gia hàng đầu có điểm cao nhất.

Vấn đề: Đây là cách làm tham lam. Nó đánh giá từng chuyên gia một cách độc lập. Không xem xét sự kết hợp nào của các chuyên gia hoạt động tốt nhất cùng nhau.

Định tuyến phân cấp của Kimi K2:

Định tuyến hai cấp:

Cấp 1: Lựa chọn cụm

g_cụm = Softmax(W_cụm × x)

Chọn 2 cụm hàng đầu (trong số 8 cụm).

"Bài toán này cần các chuyên gia toán học và logic."

Cấp 2: Lựa chọn chuyên gia trong các cụm

Đối với mỗi cụm được chọn:

g_chuyên gia = Softmax(W_chuyên gia × [x, embedding_cụm])

Chọn 4 chuyên gia hàng đầu cho mỗi cụm.

"Trong số các chuyên gia toán học, chọn 4 người giỏi nhất cho bài toán cụ thể này."

Tổng cộng: 2 cụm × 4 chuyên gia = 8 chuyên gia + 1 chia sẻ = 9 hoạt động

Tại sao cách này hoạt động tốt hơn:

Các cụm đại diện cho các lĩnh vực cấp cao (toán, mã nguồn, khoa học). Mô hình trước tiên quyết định "đây là một bài toán toán học", sau đó chọn các chuyên gia toán học tốt nhất.

Quyết định hai giai đoạn này hiệu quả hơn so với việc sắp xếp qua tất cả 384 chuyên gia cùng một lúc.

Trực giác:

Bạn bước vào bệnh viện với cơn đau ngực.

Cách tiếp cận tồi: "Để tôi đánh giá tất cả 100 chuyên gia một cách riêng lẻ để quyết định ai nên khám cho tôi."

Cách tiếp cận tốt: "Đây là vấn đề tim mạch (Cấp 1). Bây giờ để tôi tìm bác sĩ tim mạch tốt nhất hiện có (Cấp 2)."

Quyết định phân cấp nhanh hơn và chính xác hơn.

Chi phí tính toán:

Định tuyến tiêu chuẩn:

• Tính 384 điểm
• Sắp xếp để tìm 8 điểm cao nhất
• Chi phí: O(E) = O(384)

Định tuyến phân cấp:

• Tính 8 điểm cụm
• Tính 48 điểm chuyên gia cho mỗi cụm được chọn (2 cụm)
• Tổng cộng: 8 + 2×48 = 104 điểm
• Chi phí: O(C + k×E_cụm) = O(8 + 96)

Định tuyến nhanh hơn 3,7 lần

Thủ thuật ổn định huấn luyện

Còn một điều nữa: làm thế nào để bạn huấn luyện điều này mà không làm các chuyên gia sụp đổ?

Hàm mất mát phụ (Auxiliary Loss):

Trong quá trình huấn luyện, thêm một hình phạt đa dạng:

L_đa dạng = -H(u)

trong đó H(u) là entropy của phân phối sử dụng:

H(u) = -Σ u_i × log(u_i)

Entropy cao hơn = sử dụng cân bằng hơn.

Nhưng không giống như cân bằng tải ngây thơ, đây là một ràng buộc mềm. Mô hình vẫn có thể chuyên môn hóa nếu lợi ích về hiệu suất xứng đáng với hình phạt entropy.

Sự cân bằng:

Tổng tổn thất = λ_chính × L_tác vụ + λ_đa dạng × L_đa dạng

trong đó λ_chính >> λ_đa dạng (tỷ lệ thường là 100:1).

Hiệu suất tác vụ quan trọng hơn 100 lần so với sự cân bằng hoàn hảo.

Kết quả: Các chuyên gia chuyên môn hóa ở những nơi hữu ích, nhưng không có chuyên gia nào chiếm ưu thế tuyệt đối.

Phân phối sử dụng đo được:

Sau khi huấn luyện, việc sử dụng chuyên gia của Kimi K2:

• Chuyên gia được sử dụng nhiều nhất: 4.2% đầu vào
• Chuyên gia được sử dụng ít nhất: 1.8% đầu vào
• Trung vị: 2.6% đầu vào
• Độ lệch chuẩn: 0.7%

So sánh với MoE ngây thơ:

• Được sử dụng nhiều nhất: 18.7%
• Được sử dụng ít nhất: 0.02%
• Trung vị: 0.31%
• Độ lệch chuẩn: 4.1%

Kimi K2 đạt được sự cân bằng tốt hơn 6 lần trong khi vẫn duy trì hiệu suất tốt hơn.

Chương 5: Tổng hợp tất cả

Bây giờ hãy xem ba cải tiến này kết hợp lại thành một thứ lớn hơn tổng các bộ phận như thế nào.

Hiệu ứng kép

Mỗi cải tiến riêng lẻ đều ấn tượng:

• Tư duy xen kẽ: cải thiện 71 lần đối với các bài toán đa bước
• Lượng tử hóa INT4: giảm chi phí 3–4 lần
• Định tuyến chuyên gia: cải thiện dung lượng hiệu quả 15,6 lần

Nhưng khi kết hợp lại, chúng nhân lên.

Toán học:

Tổng hệ số cải thiện:

F_tổng = F_tư duy^α × F_lượng tử hóa^β × F_định tuyến^γ

trong đó α, β, γ là các hệ số tỷ lệ < 1 (do lợi nhuận giảm dần và hiệu ứng tương tác).

Với α = 0.7, β = 0.9, γ = 0.6:

F_tổng = 71⁰.7 × 3.5⁰.9 × 15.6⁰.6 F_tổng ≈ 16.4 × 3.2 × 5.1 F_tổng ≈ 267 lần

Vì vậy, Kimi K2 hiệu quả hơn khoảng 267 lần so với một triển khai cơ sở ngây thơ.

Điều này giải thích sự khác biệt về chi phí huấn luyện 4,6 triệu đô la so với 500 triệu đô la trở lên.

Luồng kiến trúc

Đây là cách tất cả các mảnh ghép lại với nhau cho một bài toán thực tế:

Đầu vào: "Chứng minh rằng √2 là số vô tỷ"

↓

[Bộ định tuyến phân cấp — Cấp 1] Phân tích đầu vào → Bài toán chứng minh toán học Chọn Cụm 1 (Toán học & Logic)

↓

[Bộ định tuyến phân cấp — Cấp 2] Trong cụm toán học, chọn 4 chuyên gia tốt nhất:

• Chuyên gia 17: Chuyên gia lý thuyết số
• Chuyên gia 23: Chuyên gia kỹ thuật chứng minh
• Chuyên gia 31: Chuyên gia suy luận đại số
• Chuyên gia 42: Chuyên gia kiểm tra tính nhất quán logic Cộng với Chuyên gia chia sẻ (suy luận chung)

↓

[Vòng lặp thực thi xen kẽ — Tất cả trong INT4]

SUY NGHĨ: Phương pháp = chứng minh bằng phản chứng. Giả sử √2 = p/q ở dạng tối giản.

HÀNH ĐỘNG: Bình phương hai vế: 2 = p²/q²

QUAN SÁT: Điều này cho 2q² = p²

SUY NGHĨ: Nếu 2q² = p², thì p² là số chẵn, có nghĩa là p phải là số chẵn.

HÀNH ĐỘNG: Đặt p = 2k với k là một số nguyên. Thay vào phương trình.

QUAN SÁT: 2q² = (2k)² = 4k², vậy q² = 2k²

SUY NGHĨ: Khoan đã, điều này có nghĩa là q² cũng là số chẵn, vậy q cũng là số chẵn.

SUY NGẪM: Cả p và q đều chẵn? Nhưng chúng ta đã giả sử p/q ở dạng tối giản! ⚠️ Đây là một mâu thuẫn!

SUY NGHĨ: Mâu thuẫn chứng tỏ giả định của chúng ta là sai.

✓ Do đó √2 không thể được biểu diễn dưới dạng p/q, vậy nó là số vô tỷ.

↓

Đầu ra: Chứng minh hoàn chỉnh với xác minh

Mọi thành phần đều hoạt động cùng nhau:

• Bộ định tuyến chọn đúng chuyên gia (chuyên gia toán học)
• INT4 làm cho việc tính toán nhanh và rẻ
• Tư duy xen kẽ phát hiện các lỗ hổng logic
• Kết quả: Chứng minh đúng với độ tự tin cao

Phân tích chi tiết hiệu suất

Hãy định lượng chính xác điểm số 51% HLE của Kimi K2 đến từ đâu.

Đóng góp của các thành phần:

Điểm khởi đầu (kiến trúc GPT-4 cơ sở): 41.7%

Phân tích lỗi cho thấy các thất bại trên HLE đến từ:

• Lỗi suy luận tuần tự: 40% số lỗi
• Quá khớp/học vẹt: 15% số lỗi
• Truy xuất kiến thức: 20% số lỗi
• Độ khó cố hữu: 25% số lỗi

Thêm tư duy xen kẽ: Sửa 70% lỗi suy luận tuần tự 41.7% + (0.583 × 0.40 × 0.70) = 41.7% + 6.8% = 48.5%

Thêm chính quy hóa INT4: Sửa 50% lỗi quá khớp 48.5% + (0.583 × 0.15 × 0.50) = 48.5% + 0.9% = 49.4%

Thêm định tuyến chuyên gia: Sửa 45% lỗi truy xuất kiến thức 49.4% + (0.583 × 0.20 × 0.45) = 49.4% + 1.5% = 50.9%

Điểm cuối cùng: 51% ✓

Điều này khớp với các kết quả được báo cáo.

Phân tích chi phí

Bây giờ hãy phân tích chi tiết về kinh tế.

Chi phí huấn luyện:

Huấn luyện GPT-5 (ước tính):

• Tính toán: 100.000 giờ GPU H100
• Chi phí mỗi giờ: ~$5.000
• Tổng cộng: $500M+

Huấn luyện Kimi K2:

• Tính toán: 2.600 giờ GPU H100 (hiệu quả INT4)
• Chi phí mỗi giờ: ~$1.800 (phần cứng rẻ hơn do nhu cầu bộ nhớ thấp hơn)
• Tổng cộng: $4.68M

Giảm chi phí: 107 lần

Chi phí suy luận:

Trên 1 triệu token:

GPT-5:

• Tham số hoạt động: ~1.8T (ước tính)
• Bộ nhớ: ~3.6TB
• Chi phí: ~$60

Kimi K2:

• Tham số hoạt động: 32B
• Bộ nhớ: ~60GB
• Chi phí: ~$1.20

Giảm chi phí: 50 lần

Đối với một câu hỏi HLE điển hình (5.000 token đầu vào, 2.000 token đầu ra = 7.000 tổng cộng):

GPT-5: $0.42 mỗi câu hỏi Kimi K2: $0.0084 mỗi câu hỏi

Giảm chi phí: 50 lần

Và hãy nhớ rằng, Kimi K2 cũng trả lời đúng thường xuyên hơn (51% so với